Description

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

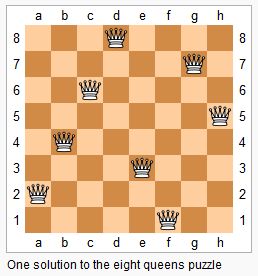
Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Input: 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below.
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Description

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Description

Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).

You may assume that the intervals were initially sorted according to their start times.

Example 1:

1
2

Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]

Example 2:

1
2
3

Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].

Java中的排序

这里介绍两种常用的排序对象：对数组的排序和对list的排序。

数组的排序

数组的排序主要采用Arrays.sort()方法，默认为升序。常用API有：

1
2
3
4
5
6
7
8
9
10

Arrays.sort(array_name,startindex,endindex);

Arrays.sort(array_name);

Arrays.sort(a3, new Comparator<people>() {
	@Override
    public int compare(people o1, people o2) {
            return Integer.compare(o1.age, o2.age);
    }
});

若想降序，可以先将数组转换为list：

1
2

List tmp = Arrays.asList(a1);
Collections.sort(tmp, Collections.reverseOrder());

List的排序

List排序主要采用Comparator类中的sort方法，主要API有：

1
2
3
4
5
6
7
8

Collections.sort(Listname);
Collections.sort(Listname, Collections.reverseOrder());
Collections.sort(l1, new Comparator<people>() {
   @Override
   public int compare(people o1, people o2) {
          return Integer.compare(o1.age, o2.age);
   }
});

可以看出两者的自定义排序均为重写compare方法。

Description

Given a collection of intervals, merge all overlapping intervals.

Example 1:

1
2
3

Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].

Example 2:

1
2
3

Input: [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considerred overlapping.

Description

Given a string s consists of upper/lower-case alphabets and empty space characters ' ', return the length of last word in the string.

If the last word does not exist, return 0.

Note: A word is defined as a character sequence consists of non-space characters only.

Example:

1
2

Input: "Hello World"
Output: 5

Description

Given a positive integer n, generate a square matrix filled with elements from 1 to n2 in spiral order.

Example:

1
2
3
4
5
6
7

Input: 3
Output:
[
 [ 1, 2, 3 ],
 [ 8, 9, 4 ],
 [ 7, 6, 5 ]
]

Description

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

1
2
3
4
5
6
7

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

1
2
3
4
5
6
7

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Description

Implement pow(x, n), which calculates x raised to the power n (xn).

Example 1:

1
2

Input: 2.00000, 10
Output: 1024.00000

Example 2:

1
2

Input: 2.10000, 3
Output: 9.26100

Example 3:

1
2
3

Input: 2.00000, -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Note:

• -100.0 < x < 100.0
• n is a 32-bit signed integer, within the range [−231, 231 − 1]

Description

Given an array of strings, group anagrams together.

Example:

1
2
3
4
5
6
7

Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

Note:

• All inputs will be in lowercase.
• The order of your output does not matter.