数据结构之红黑树

发表于 | 更新于 | 分类于

红黑树

为什么需要红黑树

红黑树首先是一棵二叉查找树，但它并不是完全平衡的，引入红黑树的目的在于相较于二叉平衡树，他维持自身所需要的旋转次数较少，统计性能较二叉平衡树更好。

主要性质

红黑树的5条性质如下：
1.每个结点要么是红的要么是黑的。
2.根结点是黑的。
3.每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的，且不含数据。
4.如果一个结点是红的，那么它的两个儿子都是黑的。
5.对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。 (black property)

2-4树（红黑树的另一种无色形式）

2-4树又称为2-3-4 树（数字代表可能的子节点个数），树中节点和存储的元素符合如下性质要求：任一节点只能是 2 度节点、3 度节点或 4 度节点，不存在元素数为 0 的节点。
2 度节点：包含 1 个元素的节点将只能有 2 个子节点；
3 度节点：包含 2 个元素的节点将只能有 3 个子节点；
4 度节点：包含 3 个元素的节点将只能有 4 个子节点；
所有叶子节点都拥有相同的深度（depth）。
元素始终保持排序顺序。

2-4 tree

2-4树转化为红黑树：

4度节点：中间的升为黑节点，其余的变为红节点

3度节点：变为一红一黑节点，红节点为黑节点的儿子

1度节点：变为黑节点

红黑树转2-4树：

将红节点并入父亲（黑节点）

基本操作

在现实实现中，节点一般包含了color,key,left,right,parent四个属性，并且将root的parent指向nil节点。

为方便理解，这里结合伪代码进行解释。

插入操作：

每次在红黑树的底部进行插入操作，并将新插入的节点颜色规定设为红色，然后再维护整棵红黑树，进行对应的重新染色或旋转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//插入函数，传入树的结构与新插入元素的引用
RB-INSERT(T,z):
	//双指针为了找到新插入元素的父节点
    y = T.nil;
    x = T.root;
	//找到插入的位置
    while x!=T.nil:
        y = x;
        if(x.key>z.key):
            x = x.left;
        else:
            x = x.right
    z.p = y;
	//树为空，作为根节点
    if(y == T.nil):
        T.root = z;
	//作为左节点或右节点
    else 
        if(z.key>y.key):
        	y.right = z;
    	else:
        	y.left = z;
	//将新插入的节点左右设空并染色为红色
    z.left = T.nil;
    z.right = T.nil;
    z.color = RED;
	//可能引发冲突，需要对红黑树进行重新染色或旋转
    RB-INSERT-FIXUP(T,z);

接下来来看红黑树的维护操作。插入一个红节点后，若其父节点为黑色，则没有冲突发生，若其父节点为红色，则违反了红黑树的性质，需要进行重新染色或旋转，这里，冲突又分为了6种情况，因为对称性，其中3种是另外3种的镜像。所以这里我们只分析3种情况。

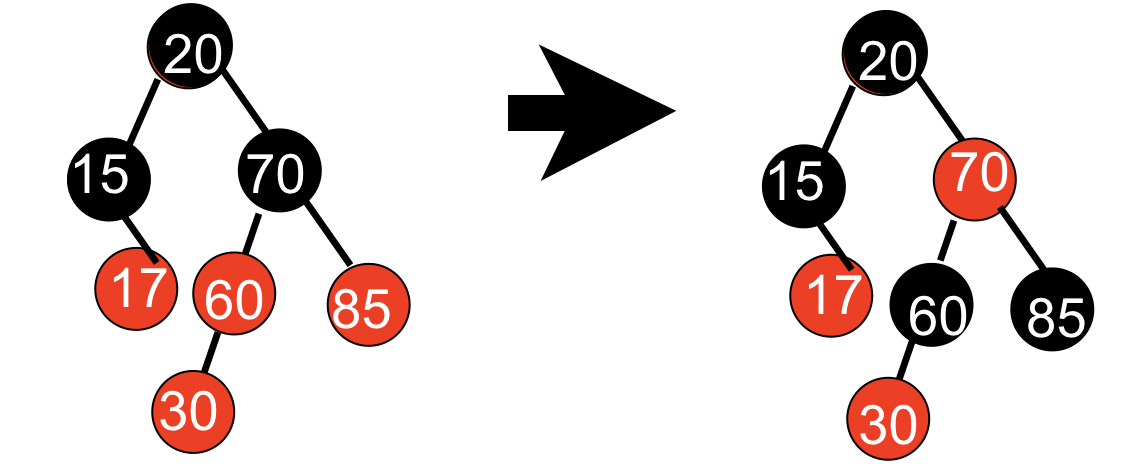
情况1：父节点为红，父节点的兄弟节点也为红

这种情况比较好处理，直接进行重新染色就好，将父节点与叔叔节点染为黑色，将爷爷节点染为红色，然后再对爷爷节点进行冲突检查与维护。

WX20181014-102511@2x

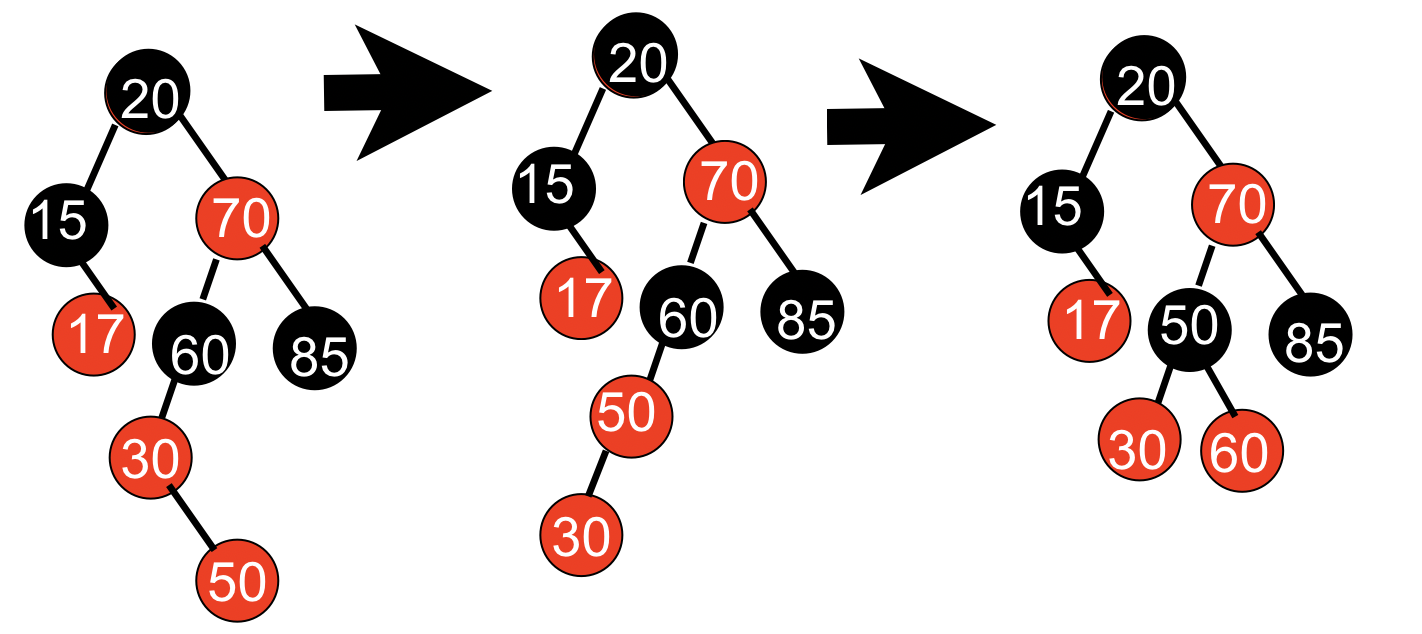
情况2：父节点为红，父节点的兄弟节点为黑或为空，其新插入节点，父节点，爷爷节点不在一条直线上。这个时候，我们需要先以父节点为旋转中心做一次旋转，将爷父孙三点先转到一条直线上，然后构成了接下来讨论的情况3。

情况3：父节点为红，父节点的兄弟节点为黑或为空，其新插入节点，父节点，爷爷节点在一条直线上。这个时候需要以爷爷节点为中心做一次旋转，使父节点成为爷孙节点的新父节点。

WX20181014-102252@2x

先来完成左旋与右旋的代码：

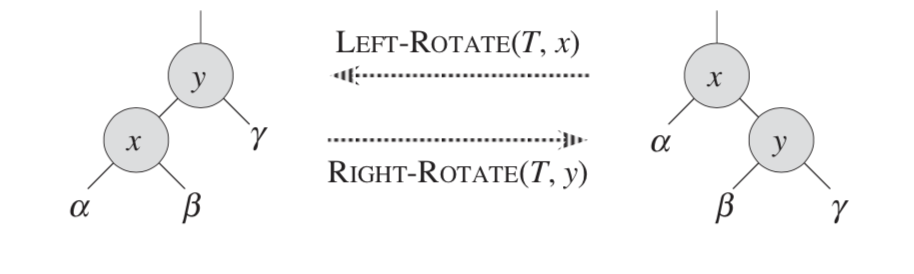
WX20181014-104356@2x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
LEFT-ROTATE(T, x):
    y = x.right             //找到新的中心节点
    x.right = y.left        //将y的左子树接到x上
    if y.left != T.nil
        y.left.p = x 
    y.p = x.p               //将x的父节点作为y的父节点
    if x.p == T.nil         
        T.root =y
    else
    	if x == x.p.left 
        	x.p.left = y
    	else 
        	x.p.right = y 
    y.left = x              //将x作为新的中心节点y的子节点
    x.p = y

RIGHT-ROTATE(T, x):
    y = x.left             //找到新的中心节点
    x.left = y.right        //将y的右子树接到x上
    if y.right != T.nil
        y.right.p = x 
    y.p = x.p               //将x的父节点作为y的父节点
    if x.p == T.nil         
        T.root =y
    else
    	if x == x.p.left 
        	x.p.left = y
    	else 
        	x.p.right = y 
    y.right = x              //将x作为新的中心节点y的子节点
    x.p = y

接下来就是维护的部分，分为6种情况来写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
RB-INSERT-FIXUP(T,z):
    while z.p.color == RED:
        if z.p == z.p.p.left:
            y = z.p.p.right;
            if y.color == RED:          //情况1
                z.p.color = BLACK;
                y.color = BLACK;
                z.p.p.color = RED;
                z = z.p.p;
            else 
                if z == z.p.right:      //情况2
                    z = z.p;
                    LEFT-ROTATE(T,z);
                z.p.color = BLACK;      //情况3，先染色再旋转
                z.p.p.color = RED;
                RIGHT-ROTATE(T,z.p.p);
        else:
            y = z.p.p.left;
            if y.color == RED:          //镜像情况1
                z.p.color = BLACK;
                y.color = BLACK;
                z.p.p.color = RED;
                z = z.p.p;
            else:
                if z == z.p.left:       //镜像情况2
                    z = z.p;
                    RIGHT-ROTATE(T,z);
                z.p.color = BLACK;      //镜像情况3
                z.p.p.color = RED;
                LEFT-ROTATE(T,z.p.p);
    T.root.color = BLACK;               //确保根节点为黑

删除操作

未完待续